[알고리즘] Java로 DFS, BFS구현하기

DFS란?

DFS란 Depth First Search의 약자로 하나의 정점을 깊게 파고들어 탐색하는 방식입니다.
스택을 이용하여 구현할 수 있으며, 재귀 함수의 특징을 통한 구현이 일반적입니다.

BFS란?

BFS란 Breadth First Search의 약자로 DFS처럼 하나의 경로를 깊게 탐색하지 않고 넓게 검사합니다.
큐를 이용하여 구현할 수 있습니다.

구현 전체 코드 (Java)

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

/* 인접행렬 그래프 클래스
 * nV: 정점. Vertex의 개수
 * nE: 간선. Edge의 개수
 */
class AdjGraph{
	private int nV;
	private int[][] graph;
	private boolean[] hasVisited;
	
	//생성자
	public AdjGraph(int nV) {
		//멤버변수 초기화
		this.nV = nV;
		this.graph = new int[nV+1][nV+1];
		this.hasVisited = new boolean[nV+1];
	}
	
	//양방향 간선 추가
	public void add(int x, int y) {
		graph[x][y] = 1;
		graph[y][x] = 1;
	}
	
	//단방향 간선 추가
	public void addSingle(int x, int y) {
		graph[x][y] = 1;
	}
	
	
	//visited 초기화
	public void clear() {
		for(int i=1; i<=nV; i++) {
			hasVisited[i] = false;
		}
	}
	
	//인접행렬 출력
	public void print() {
		System.out.println("= 인접행렬 출력 =");
        for(int i=0; i<graph.length; i++) {
            for(int j=0; j<graph[i].length; j++)
                System.out.print(graph[i][j] + " ");
            System.out.println();
        }
	}
	
	//DFS Logic
	public void dfs(int idx) {
		//dfs()에 들어온 정점을 방문처리한다.
		hasVisited[idx] = true;
		System.out.print(idx + " ");
		
		/*
		 * i가 1부터 끝까지 돌며 자신과 연결된 정점을 찾음.
		 * 정점을 찾았다면 잠시 함수를 멈추고 다음 dfs(i)를 실행했다가 처리가 모두 완료되면 돌아옴.
		 * 따라서 깊이우선탐색이 가능함.
		 */
		for(int i=1; i<=nV; i++) {
			//연결이 되어있고 해당 정점이 미방문일경우.
            if(graph[idx][i] == 1 && hasVisited[i] == false)
            	dfs(i);
		}
	}
	
	//BFS Logic
	public void bfs(int idx) {
		Queue<Integer> queue = new LinkedList<>();
		
		// queue에 시작 정점 추가.
		queue.add(idx);
		hasVisited[idx] = true;
		
		while( !queue.isEmpty() ) {
			// poll: pop하고 pop된 값 반환
			idx = queue.poll();
			System.out.print(idx + " ");
			
			for(int i=1; i<=nV; i++) {
				if (graph[idx][i] == 1 && hasVisited[i] == false) {
					//queue에 인접 정점 삽입
					queue.add(i);
					//방문처리
					hasVisited[i] = true;
				}
			}
			
		}
	}
	
}

// Main이 있는 클래스
public class GraphViewer {
	//멤버변수
	int nV;
	int nE;
	AdjGraph graph;
	
	//생성자
	public GraphViewer() {
		Scanner sc = new Scanner(System.in);
		//정점의 개수 받기
		nV = sc.nextInt();
		//간선의 개수 받기
		nE = sc.nextInt();
		//그래프 초기화
		graph = new AdjGraph(nV);
		
		//graph에 간선 추가하기.
		for(int i=0; i<nE; i++)
			graph.add(sc.nextInt(), sc.nextInt());
		
		//인접행렬 프린트하기
		graph.print();
		
		//DFS로 출력
		System.out.print("DFS로 정점 1부터 탐색한 결과: ");
		graph.dfs(1);
		
		//BFS로 출력. clear로 visited 초기화
		graph.clear();
		System.out.print("BFS로 정점 1부터 탐색한 결과: ");
		graph.bfs(1);
		
		sc.close();
	}
	
	//메인 메서드
	public static void main(String[] args) {
		GraphViewer gv = new GraphViewer();
	}
}

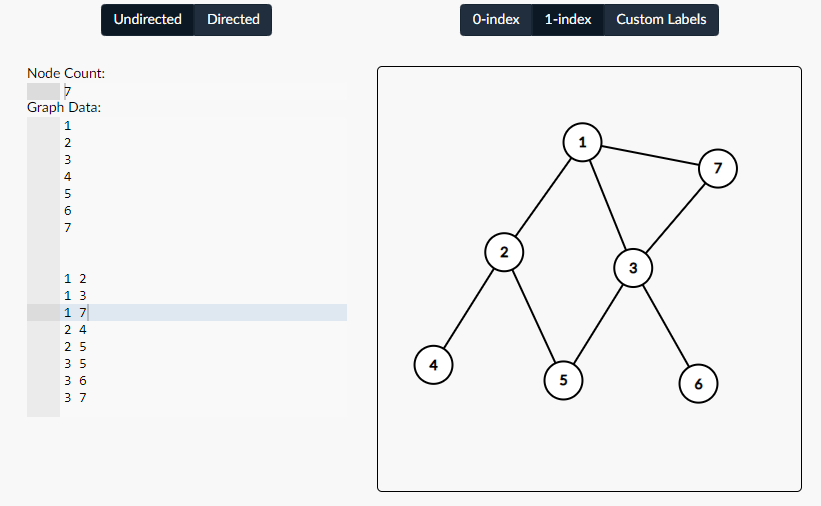
그래프 & 실행 결과

Graph 그리는 사이트